Trong bài viết này, mình sẽ hướng dẫn các bạn cách tìm các khoản đầu tư vốn tối ưu hóa tổng lợi nhuận trong Excel.
| Tham gia kênh Telegram của AnonyViet 👉 Link 👈 |
Xây dựng mô hình tìm các khoản đầu tư tối ưu hóa lợi nhuận
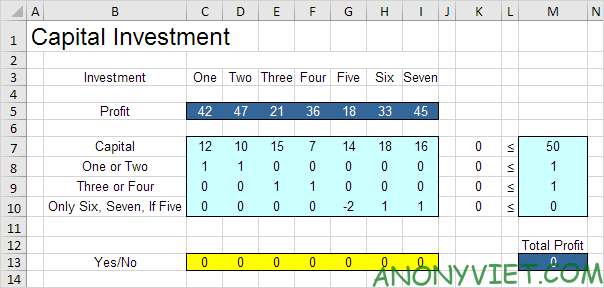
Mô hình chúng ta sẽ giải quyết trông như sau trong Excel.
1. Để tạo mô hình lập trình số nguyên nhị phân (BIP) này, hãy trả lời ba câu hỏi sau:
a. Các quyết định sẽ được thực hiện là gì? Đối với vấn đề này, chúng ta cần Excel tìm ra những khoản đầu tư vốn nào cần thực hiện (Có = 1, Không = 0).
b. Những ràng buộc đối với các quyết định này là gì? Thứ nhất, số vốn sử dụng của các khoản đầu tư không được vượt quá số vốn hạn chế hiện có (50). Ví dụ, đầu tư One sử dụng 12 đơn vị vốn. Thứ hai, chỉ có thể đầu tư One hoặc đầu tư Two. Thứ ba, chỉ có thể đầu tư Three hoặc đầu tư Four. Thứ tư, đầu tư Six và đầu tư Seven chỉ có thể được thực hiện nếu đầu tư Five được thực hiện.
c. Thước đo tổng thể về hiệu suất cho những quyết định này là gì? Thước đo tổng thể về hiệu suất là tổng lợi nhuận của các khoản đầu tư vốn được thực hiện, vì vậy mục tiêu là tối đa hóa số lượng này.
2. Để làm cho mô hình dễ hiểu hơn, hãy tạo các phạm vi được đặt tên như sau.
| Range Name | Cells |
|---|---|
| Profit | C5:I5 |
| YesNo | C13:I13 |
| TotalProfit | M13 |
3. Chèn năm hàm SUMPRODUCT sau đây.
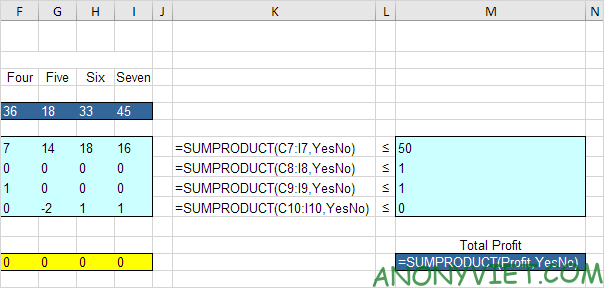
Giải thích: ô K7 (số vốn được sử dụng) bằng tổng sản phẩm của phạm vi C7:I7 và YesNo, ô K8 bằng tổng sản phẩm của phạm vi C8:I8 và YesNo,… Tổng lợi nhuận (Total Profit) bằng kết quả của lợi nhuận và YesNo.
Thử bảng và tìm lỗi sai
Với công thức này, việc phân tích bất kỳ dung dịch thử nào trở nên dễ dàng.
1. Ví dụ, nếu chúng ta thực hiện đầu tư One và Two, ràng buộc thứ hai sẽ bị vi phạm.
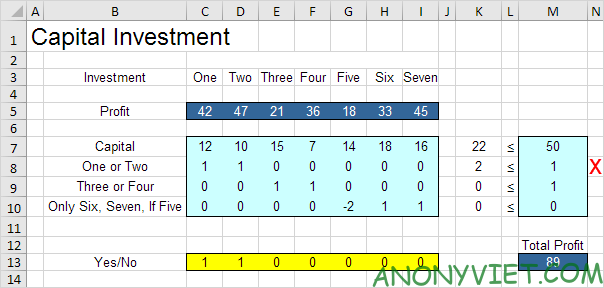
2. Ví dụ, nếu chúng ta thực hiện đầu tư Six và Seven, mà không thực hiện đầu tư Five, thì ràng buộc thứ tư sẽ bị vi phạm.
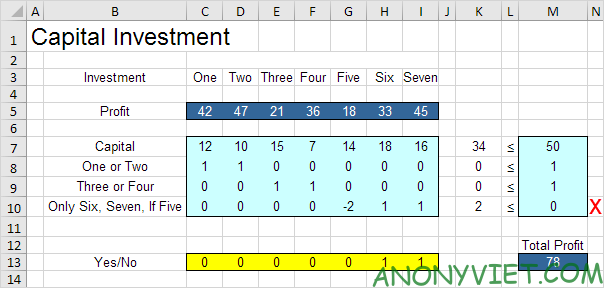
3. Tuy nhiên, bạn nên đầu tư One, Five và Six. Tất cả các ràng buộc đều được thỏa mãn.
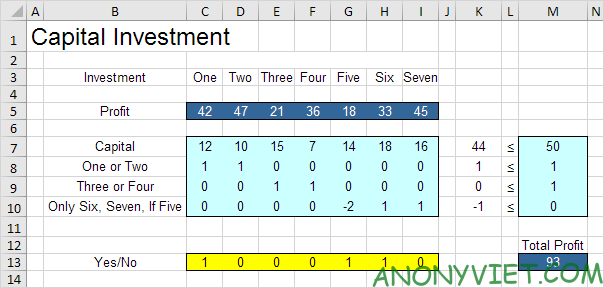
Tiếp theo, mình sẽ mô tả cách sử dụng Excel Solver để nhanh chóng tìm ra giải pháp tối ưu.
Giải quyết mô hình
1. Trên tab Data, trong nhóm Analyze, hãy bấm Solver.

Nhập dữ liệu như hình dưới.
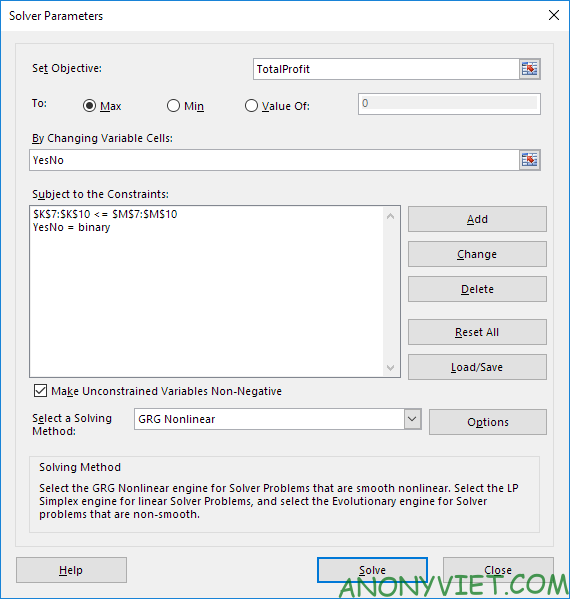
2. Nhập TotalProfit trong Objective.
3. Chọn Max.
4. Nhập YesNo trong ô By Changing Variable Cells.
5. Nhấp vào Add để nhập ràng buộc sau.
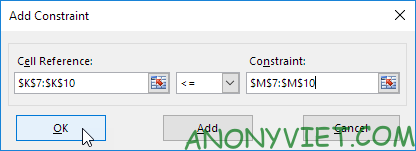
6. Nhấp vào Add để nhập ràng buộc sau.
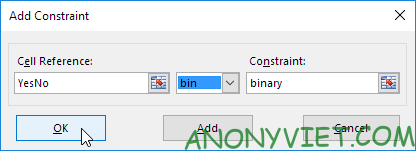
7. Chọn ‘Make Unconstrained Variables Non-Negative’ và chọn ‘Simplex LP’.
8. Cuối cùng, nhấp vào Solve.
Kết quả:
Giải pháp tối ưu:
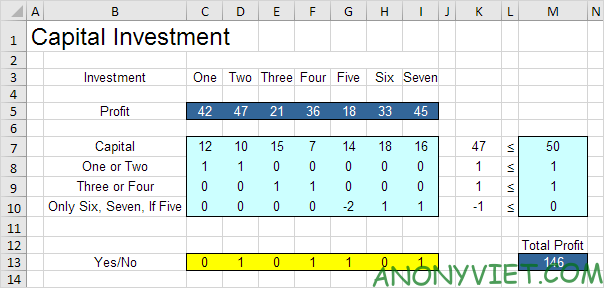
Kết luận: đầu tư Two, Four, Five và Seven là tối ưu. Giải pháp này cho lợi nhuận tối đa là 146. Tất cả các ràng buộc đều được thỏa mãn.
Ngoài ra, bạn cũng có thể xem nhiều bài excel khác tại đây.
Câu hỏi thường gặp
Tôi có cần kỹ năng Excel nâng cao để sử dụng phương pháp này không?
Không cần thiết. Bài viết hướng dẫn chi tiết từng bước, từ xây dựng mô hình đến sử dụng công cụ Solver trong Excel. Chỉ cần có kiến thức cơ bản về Excel là bạn đã có thể thực hiện được.
Solver trong Excel có luôn tìm ra được giải pháp tối ưu không?
Tùy thuộc vào mô hình và ràng buộc bạn đặt ra. Solver sẽ tìm ra giải pháp tối ưu *trong phạm vi* các ràng buộc được định nghĩa. Nếu mô hình không được thiết lập chính xác hoặc có ràng buộc quá chặt, Solver có thể không tìm được giải pháp hoặc tìm được giải pháp không tối ưu.
Tôi có thể áp dụng phương pháp này cho các vấn đề đầu tư khác ngoài ví dụ trong bài viết không?
Hoàn toàn được. Phương pháp này là một mô hình tổng quát. Bạn chỉ cần thay đổi dữ liệu đầu vào (lợi nhuận, vốn đầu tư, ràng buộc) cho phù hợp với tình huống đầu tư cụ thể của mình.